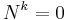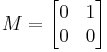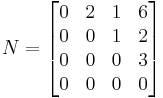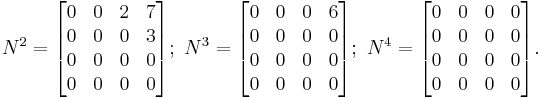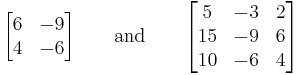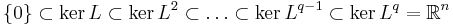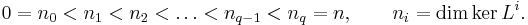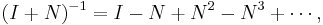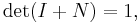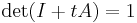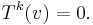Nilpotent matrix

In linear algebra, a nilpotent matrix is a square matrix N such that

$N^k = 0\,$

for some positive integer k. The smallest such k is sometimes called the degree of N.

More generally, a nilpotent transformation is a linear transformation L of a vector space such that L^k = 0 for some positive integer k (and thus, L^j = 0 for all j ≥ k). Both of these concepts are special cases of a more general concept of nilpotence that applies to elements of rings.

1 Examples
2 Characterization
3 Classification
4 Flag of subspaces
5 Additional properties
6 Generalizations
7 References
8 External links

Examples

The matrix

$M = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}$

is nilpotent, since M² = 0. More generally, any triangular matrix with 0s along the main diagonal is nilpotent. For example, the matrix

$N = \begin{bmatrix} 0 & 2 & 1 & 6\\ 0 & 0 & 1 & 2\\ 0 & 0 & 0 & 3\\ 0 & 0 & 0 & 0 \end{bmatrix}$

is nilpotent, with

$N^2 = \begin{bmatrix} 0 & 0 & 2 & 7\\ 0 & 0 & 0 & 3\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} ;\ N^3 = \begin{bmatrix} 0 & 0 & 0 & 6\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} ;\ N^4 = \begin{bmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix}.$

Though the examples above have a large number of zero entries, a typical nilpotent matrix does not. For example, the matrices

$\begin{bmatrix} 6 & -9 \\ 4 & -6 \end{bmatrix}\qquad\text{and}\qquad \begin{bmatrix} 5 & -3 & 2 \\ 15 & -9 & 6 \\ 10 & -6 & 4 \end{bmatrix}$

both square to zero, though neither matrix has zero entries.

Characterization

For an n × n square matrix N with real (or complex) entries, the following are equivalent:

N is nilpotent.
The minimal polynomial for N is λ^k for some positive integer k ≤ n.
The characteristic polynomial for N is λⁿ.
The only (complex) eigenvalue for N is 0.
tr(N^k) = 0 for all k > 0.

The same theorem holds true for matrices over any field.

This theorem has several consequences, including:

The degree of an n × n nilpotent matrix is always less than or equal to n. For example, every 2 × 2 nilpotent matrix squares to zero.
The determinant and trace of a nilpotent matrix are always zero.
The only nilpotent diagonalizable matrix is the zero matrix.

Classification

Consider the n × n shift matrix:

$S = \begin{bmatrix} 0 & 1 & 0 & \ldots & 0 \\ 0 & 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \\ 0 & 0 & 0 & \ldots & 0 \end{bmatrix}.$

This matrix has 1s along the superdiagonal and 0s everywhere else. As a linear transformation, the shift matrix “shifts” the components of a vector one slot to the left:

$S(x_1,x_2,\ldots,x_n) = (x_2,\ldots,x_n,0).$

This matrix is nilpotent with degree n, and is the “canonical” nilpotent matrix.

Specifically, if N is any nilpotent matrix, then N is similar to a block diagonal matrix of the form

$\begin{bmatrix} S_1 & 0 & \ldots & 0 \\ 0 & S_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & S_r \end{bmatrix}$

where each of the blocks S₁, S₂, ..., S_r is a shift matrix (possibly of different sizes). This theorem is a special case of the Jordan canonical form for matrices.

For example, any nonzero 2 × 2 nilpotent matrix is similar to the matrix

$\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}.$

That is, if N is any nonzero 2 × 2 nilpotent matrix, then there exists a basis b₁, b₂ such that Nb₁ = 0 and Nb₂ = b₁.

This classification theorem holds for matrices over any field. (It is not necessary for the field to be algebraically closed.)

Flag of subspaces

A nilpotent transformation L on Rⁿ naturally determines a flag of subspaces

$\{0\} \subset \ker L \subset \ker L^2 \subset \ldots \subset \ker L^{q-1} \subset \ker L^q = \mathbb{R}^n$

and a signature

$0 = n_0 < n_1 < n_2 < \ldots < n_{q-1} < n_q = n,\qquad n_i = \dim \ker L^i.$

The signature characterizes L up to an invertible linear transformation. Furthermore, it satisfies the inequalities

$n_{j%2B1} - n_j \leq n_j - n_{j-1}, \qquad \mbox{for all } j = 1,\ldots,q-1.$

Conversely, any sequence of natural numbers satisfying these inequalities is the signature of a nilpotent transformation.

Additional properties

If N is nilpotent, then I + N is invertible, where I is the n × n identity matrix. The inverse is given by

$(I %2B N)^{-1} = I - N %2B N^2 - N^3 %2B \cdots,$

where only finitely many terms of this sum are nonzero.

If N is nilpotent, then

$\det (I %2B N) = 1,\!\,$

where I denotes the n × n identity matrix. Conversely, if A is a matrix and

$\det (I %2B tA) = 1\!\,$

for all values of t, then A is nilpotent.

Every singular matrix can be written as a product of nilpotent matrices.^[1]

Generalizations

A linear operator T is locally nilpotent if for every vector v, there exists a k such that

$T^k(v) = 0.\!\,$

For operators on a finite-dimensional vector space, local nilpotence is equivalent to nilpotence.

References

^ R. Sullivan, Products of nilpotent matrices, Linear and Multilinear Algebra, Vol. 56, No. 3

External links

Nilpotent matrix and nilpotent transformation on PlanetMath.